算法训练营（day55）

动态规划理论基础

动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

举个例子：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划中 dp[j] 是由 dp[j-weight[i]] 推导出来的，然后取 max(dp[j], dp[j - weight[i]] + value[i])。

动态规划的解题步骤

  1. 确定 dp 数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp 数组如何初始化
  4. 确定遍历顺序
  5. 举例推导 dp 数组

583. 两个字符串的删除操作

题目链接：https://leetcode.cn/problems/delete-operation-for-two-strings/description/

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

解题思路

思路一：

解题过程：动态规划

按照动规五部曲来分析：

  1. 确定dp数组（dp table）以及下标的含义

​ dp[j]表示容量为j的背包，最多可以背最大重量为dp[j]

​ 本题的 dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数

  1. 确定递推公式
  • word1[i - 1] 与 word2[j - 1] 相同，则dp[i][j] = dp[i - 1][j - 1]
  • word1[i - 1]与 word2[j - 1] 不相同，则有三种情况：
    • 删word1[i - 1]，则 dp[i][j] = dp[i - 1][j] + 1
    • 删word2[j - 1] ，则 dp[i][j] = dp[i][j - 1] + 1
    • 同时删 word1[i - 1] 和 word2[j - 1]，则 dp[i][j] = dp[i - 1][j - 1] + 2

​ 最后取最小值得到递推公式是：

1
2
3
4
5
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
    dp[i][j] = dp[i - 1][j - 1];
}else{ 
    dp[i][j] = Math.min(Math.min(dp[i][j - 1] + 1, dp[i -1][j] + 1), dp[i - 1][j - 1] + 2);
}

  1. dp数组的初始化

    dp[i][0]：当word2为空字符串，以 i-1 为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i 。

    dp[0][j] 的话同理，所以dp数组的初始化为：

1
2
3
4
5
6
7
int[][] dp = new int[m + 1][n + 1];
for(int i = 0; i <= m; i++){
    dp[i][0] = i;
}
for(int j = 0; j <= n; j++){
    dp[0][j] = j;
}
  1. 确定遍历顺序

​ 根据递推公式可以得出，dp[i][j] 依赖于dp[i - 1][j - 1] 、 dp[i][j - 1] 和 dp[i - 1][j]，是从前到后，从左往右遍历的一个 矩阵

1
2
3
4
5
6
7
8
9
for(int i = 1; i < m + 1; i++){
    for(int j = 1; j < n + 1; j++){
        if(word1.charAt(i - 1) == word2.charAt(j - 1)){
            dp[i][j] = dp[i - 1][j - 1];
        }else{ 
            dp[i][j] = Math.min(Math.min(dp[i][j - 1] + 1, dp[i -1][j] + 1), dp[i - 1][j - 1] + 2);
        }
    }
}
  1. 推导dp数组

思路二：

解题过程：动态规划

只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

详细代码

解法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        for(int i = 0; i <= m; i++){
            dp[i][0] = i;
        }
        for(int j = 0; j <= n; j++){
            dp[0][j] = j;
        }

        for(int i = 1; i < m + 1; i++){
            for(int j = 1; j < n + 1; j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{ 
                    dp[i][j] = Math.min(Math.min(dp[i][j - 1] + 1, dp[i -1][j] + 1), dp[i - 1][j - 1] + 2);
                }
            }
        }
        return dp[m][n];
    }
}

解法二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];

        for(int i = 1; i < m + 1; i++){
            for(int j = 1; j < n + 1; j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{ 
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return m + n - 2 * dp[m][n];
    }
}

72. 编辑距离

题目链接：https://leetcode.cn/problems/edit-distance/description/

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

解题思路

解题过程：动态规划

按照动规五部曲来分析：

  1. 确定dp数组（dp table）以及下标的含义

​ dp[j]表示容量为j的背包，最多可以背最大重量为dp[j]

​ 本题的 dp[i][j]：以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离

  1. 确定递推公式
  • word1[i - 1] 与 word2[j - 1] 相同，则dp[i][j] = dp[i - 1][j - 1]
  • word1[i - 1]与 word2[j - 1] 不相同，则有三种情况：
    • 删word1[i - 1]，则 dp[i][j] = dp[i - 1][j] + 1
    • 删word2[j - 1] ，则 dp[i][j] = dp[i][j - 1] + 1
    • 替换 word1[i - 1] ，则 dp[i][j] = dp[i - 1][j - 1] + 1

​ 最后取最小值得到递推公式是：

1
2
3
4
5
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
    dp[i][j] = dp[i - 1][j - 1];
}else{
    dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1));
}

  1. dp数组的初始化

    dp[i][0]：当word2为空字符串，以 i-1 为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i 。

    dp[0][j] 的话同理，所以dp数组的初始化为：

1
2
3
4
5
6
7
int[][] dp = new int[m + 1][n + 1];
for(int i = 0; i <= m; i++){
    dp[i][0] = i;
}
for(int j = 0; j <= n; j++){
    dp[0][j] = j;
}
  1. 确定遍历顺序

​ 从四个递推公式可以看出，dp[i][j] 依赖于dp[i - 1][j - 1] 、 dp[i][j - 1] 和 dp[i - 1][j]，是从前到后，从左往右遍历的一个 矩阵

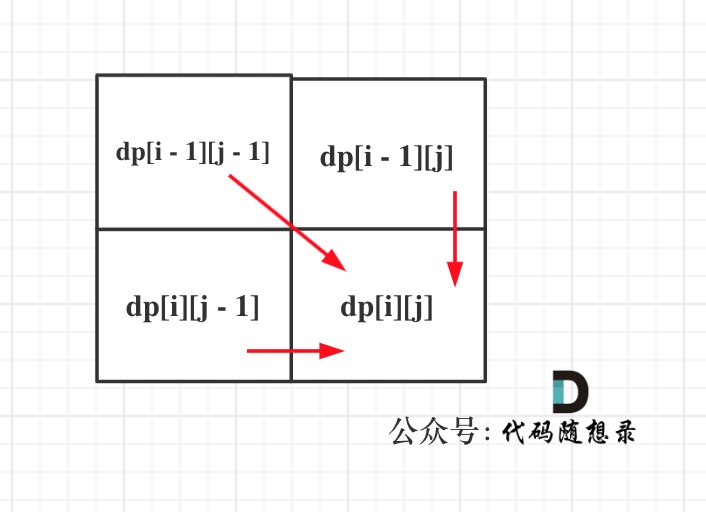
72.编辑距离 
1
2
3
4
5
6
7
8
9
for(int i = 1; i < m + 1; i++){
    for(int j = 1; j < n + 1; j++){
        if(word1.charAt(i - 1) == word2.charAt(j - 1)){
            dp[i][j] = dp[i - 1][j - 1];
        }else{
            dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1));
        }
    }
}
  1. 推导dp数组

详细代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        for(int i = 0; i <= m; i++){
            dp[i][0] = i;
        }
        for(int j = 0; j <= n; j++){
            dp[0][j] = j;
        }

        for(int i = 1; i < m + 1; i++){
            for(int j = 1; j < n + 1; j++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1));
                }
            }
        }
        return dp[m][n];
    }
}