算法训练营（day45）

动态规划理论基础

动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

举个例子：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划中 dp[j] 是由 dp[j-weight[i]] 推导出来的，然后取 max(dp[j], dp[j - weight[i]] + value[i])。

动态规划的解题步骤

  1. 确定 dp 数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp 数组如何初始化
  4. 确定遍历顺序
  5. 举例推导 dp 数组

01背包理论基础

01背包的主要出题方式是：有n件物品和一个最多能背重量为 w 的背包。第 i 件物品的重量是 weight[i]，得到的价值是 value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动规五部曲分析

  1. 确定dp数组（dp table）以及下标的含义

    对于背包问题，有一种写法是使用二维数组，即**dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少**。

  2. 确定递推公式

    dp[i][j]由两种方式获得：

    • 不放物品i：由dp[i - 1][j]推出，即背包容量为 j ，里面不放物品 i 的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
    • 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为 j - weight[i] 的时候不放物品 i 的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品 i 得到的最大价值

​ 所以递归公式为： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

  1. dp数组的初始化

    从 dp[i][j]的定义出发：

    • dp[i][0]，即背包容量j为0，无论是选取哪些物品，背包价值总和一定为0
    • dp[0][j]，即存放物品编号i为0的时候，各个容量的背包所能存放的最大价值
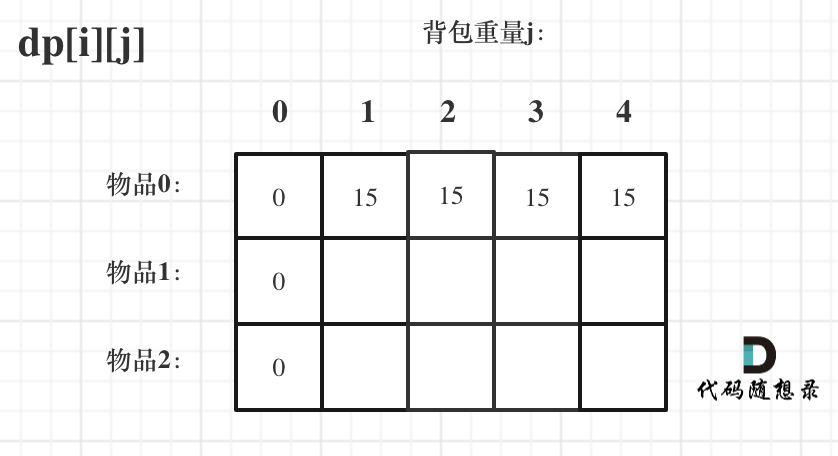
动态规划-背包问题7

  1. 确定遍历顺序

    遍历的维度有两个：物品i 与 背包重量j

    先遍历物品 还是 先遍历背包重量 其实都可以！！ 但是先遍历物品更好理解。

  2. 推导dp数组

01背包测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class BagProblem {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 动态规划获得结果
     * @param weight  物品的重量
     * @param value   物品的价值
     * @param bagSize 背包的容量
     */
    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods][bagSize + 1];

        // 初始化dp数组
        // 创建数组后，其中默认的值就是0
        for (int j = weight[0]; j <= bagSize; j++) {
            dp[0][j] = value[0];
        }

        // 填充dp数组
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i-1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }

        // 打印dp数组
        for (int i = 0; i < goods; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}

滚动数组

滚动数组，就是把二维dp降为一维dp，我们重温一下：dp[i][j] 里的i和j表达的是i是物品，j是背包容量

  1. 在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
  2. 如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：**dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);**
  3. 再简化一下表达式，只用一个一维数组 dp[j]

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

所以递归公式为：

1
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

滚动数组遍历背包顺序

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

倒序遍历是为了保证物品i只被放入一次！！！

一维dp遍历一定要 先物品后背包容量 吗？

答案：是的！！！

一维dp的写法中，背包容量一定是要倒序遍历的，如果遍历背包容量放在上一层，那么每个 dp[j] 就只会放入一个物品，即：背包里只放入了一个物品。

倒序遍历的原因，本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。

(个人理解：一维dp就是先放大的，大的塞进去还有位置就再补小的，大的塞不进就换小一号的塞，保证自己不会犯糊涂，塞了两个一样小的充当一个大的用)

完全背包理论基础

完全背包问题的出题方式是：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。而解决01背包和完全背包唯一不同就是体现在遍历顺序上。

面试题：对于纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后在问，两个for循环的先后是否可以颠倒？为什么？

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！，具体分析参考：完全背包理论基础

对于实际情况，具体问题需要具体分析，一般情况下没有 纯完全背包问题 的提问方式，都需要对问题进行分析，选择 合适的遍历顺序 进行解题。

完全背包测试代码

组合不强调元素之间的顺序，排列强调元素之间的顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//先遍历物品，再遍历背包（用于求组合数）
private static void testCompletePack(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 0; i < weight.length; i++){ // 遍历物品
        for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//先遍历背包，再遍历物品（用于求排列数）
private static void testCompletePackAnotherWay(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
        for (int j = 0; j < weight.length; j++){ // 遍历物品
            if (i - weight[j] >= 0){
                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
            }
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

70. 爬楼梯

题目链接：https://leetcode.cn/problems/climbing-stairs/description/

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

解题思路

解题过程：动态规划

按照动规五部曲来分析：

  1. 确定dp数组（dp table）以及下标的含义

​ dp[j]表示容量为j的背包，最多可以背最大重量为dp[j]

​ 本题的 dp[j]：爬到有j个台阶的楼顶，有dp[j]种方法

  1. 确定递推公式

    由 组合数 联系到递归公式：dp[j] += dp[j - nums[i]]

​ 本题的递推公式为：**dp[i] += dp[i - j];**

  1. dp数组的初始化

    由 组合数 联系到 dp[0] 一定要为1，dp[0] = 1 是 递归公式的基础

    下标非0的 dp[i]初始化为0，因为 dp[i] 是靠 dp[i-j] 累计上来的，dp[i]本身为0这样才不会影响结果。

  2. 确定遍历顺序

​ 本题求爬楼梯的方法，是求 排列数

​ 组合不强调元素之间的顺序，排列强调元素之间的顺序，最终输出结果是 组合数 还是 排列数 和 两个for循环的先后顺序 紧密联系

  • 外层for循环遍历背包（总楼层），内层for遍历物品（台阶数） [排列数]

​ 完全背包问题，内循环需要从前向后遍历

1
2
3
4
5
for (int i = 0; i <= n; i++) {
       for (int j = 0; j < weight.length; j++) {
           if (i >= weight[j]) dp[i] += dp[i - weight[j]];
       }
   }

​ 此时dp[i]里算出来的就是排列数！

  1. 推导dp数组

详细代码

之前使用的是递归方法：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

下面使用完全背包的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        int[] weight = {1, 2};
        dp[0] = 1;

        for(int i = 1; i <= n; i++){
            for(int j = 0; j < weight.length; j++){
                if(i - weight[j] >= 0){
                    dp[i] += dp[i - weight[j]];
                }
            }
        }
        return dp[n];
    }
}

322. 零钱兑换

题目链接：https://leetcode.cn/problems/coin-change/description/

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

解题思路

解题过程：动态规划

按照动规五部曲来分析：

  1. 确定dp数组（dp table）以及下标的含义

​ dp[j]表示容量为j的背包，最多可以背最大重量为dp[j]

​ 本题的 dp[j] 表示为凑足总额为j所需钱币的最少个数

  1. 确定递推公式

    凑足总额为 j - coins[i]的最少个数为 dp[j - coins[i]]，那么只需要加上一个钱币 coins[i]即dp[j - coins[i]] + 1 就是 dp[j]（考虑coins[i]）

    所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。

    递推公式：**dp[j] = min(dp[j - coins[i]] + 1, dp[j]);**

  2. dp数组的初始化

    凑足总金额为0所需钱币的个数一定是0，那么 dp[0] = 0;

    考虑到递推公式的特性，dp[j] 必须初始化为一个最大的数，否则就会在 min(dp[j - coins[i]] + 1, dp[j]) 比较的过程中被初始值覆盖。

    所以下标非0的元素都是应该是最大值。

  3. 确定遍历顺序

​ 组合不强调元素之间的顺序，排列强调元素之间的顺序，最终输出结果是 组合数 还是 排列数 和 两个for循环的先后顺序 紧密联系

​ 本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的

​ 本题采用的是 外层for循环遍历物品（钱币），内层for遍历背包（金钱总额） [组合数]

1
2
3
4
5
6
7
for(int i = 0; i < coins.length; i++){
       for(int j = coins[i]; j <= amount; j++){
           if(dp[j - coins[i]] != max){
               dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
           }
       }
   }
  1. 推导dp数组

详细代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int coinChange(int[] coins, int amount) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[amount + 1];
        for(int j = 0; j < dp.length; j++){
            dp[j] = max;
        }
        dp[0] = 0;

        for(int i = 0; i < coins.length; i++){
            for(int j = coins[i]; j <= amount; j++){
                if(dp[j - coins[i]] != max){
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        return dp[amount] == max ? -1 : dp[amount];
    }
}

279. 完全平方数

题目链接：https://leetcode.cn/problems/perfect-squares/description/

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

解题思路

解题过程：动态规划

按照动规五部曲来分析：

  1. 确定dp数组（dp table）以及下标的含义

​ dp[j]表示容量为j的背包，最多可以背最大重量为dp[j]

​ 本题的 dp[j] 表示为 和为j的完全平方数的最少数量

  1. 确定递推公式

    dp[j] 可以由 dp[j - i * i]推出， dp[j - i * i] + 1 便可以凑成 dp[j]。

    此时我们要选择最小的 dp[j]

    所以递推公式为：**dp[j] = min(dp[j - i * i] + 1, dp[j]);**

  2. dp数组的初始化

    dp[0] 表示 和为0的完全平方数的最小数量，那么 dp[0] 一定是0

    从递归公式 dp[j] = min(dp[j - i * i] + 1, dp[j]) 中可以看出每次 dp[j] 都要选最小的，所以非0下标的 dp[j] 一定要初始为最大值，这样 dp[j] 在递推的时候才不会被初始值覆盖。

  3. 确定遍历顺序

​ 组合不强调元素之间的顺序，排列强调元素之间的顺序，最终输出结果是 组合数 还是 排列数 和 两个for循环的先后顺序 紧密联系

​ 本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！

  • 外层for循环遍历物品（i * i），内层for遍历背包（总数）
1
2
3
4
5
6
7
8
9
// 遍历物品
for (int i = 1; i * i <= n; i++) {
       // 遍历背包
       for (int j = i * i; j <= n; j++) {
           if (dp[j - i * i] != max) {
               dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
           }
       }
   }
  • 外层for循环遍历背包（总数），内层for遍历物品（i * i）
1
2
3
4
5
6
7
// 遍历背包
for (int j = 1; j <= n; j++) {
       // 遍历物品
       for (int i = 1; i * i <= j; i++) {
           dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
       }
   }
  1. 推导dp数组

详细代码

解法一：外层for循环遍历背包（总数），内层for遍历物品（i * i）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numSquares(int n) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[n + 1];
        for(int j = 0; j <= n; j++){
            dp[j] = max;
        }
        dp[0] = 0;

        for(int j = 1; j <= n; j++){
            for(int i = 1; i * i <= j; i++){
                dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
            }
        }
        return dp[n];
    }
}

解法二：外层for循环遍历物品（i * i），内层for遍历背包（总数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int numSquares(int n) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[n + 1];
        for(int j = 0; j <= n; j++){
            dp[j] = max;
        }
        dp[0] = 0;

        for(int i = 1; i * i <= n; i++){
            for(int j = i * i; j <= n; j++){
                if(dp[j - i * i] != max){
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                }
            }
        }
        return dp[n];
    }
}