算法训练营（day17）

110. 平衡二叉树

题目链接：https://leetcode.cn/problems/balanced-binary-tree/description/

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

解题思路

解题过程：

思路一：递归

• 直接计算 left 和 right 节点的高度

• 如果左右节点高度差大于1，返回false

思路二：迭代（层序遍历）&& 优化（理解即可）

• 迭代法计算高度时会重复遍历，效率较低，理解即可

详细代码

解法一：递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeightDFS(root) != -1;
    }

    public int getHeightDFS(TreeNode node){
        if(node == null){
            return 0;
        }

        int leftHeight = getHeightDFS(node.left);
        if(leftHeight == -1){
            return -1;
        }
        int rightHeight = getHeightDFS(node.right);
        if(rightHeight == -1){
            return -1;
        }
        if(Math.abs(leftHeight - rightHeight) > 1){
            return - 1;
        }
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

解法二：层序遍历迭代

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
   /**
     * 迭代法，效率较低，计算高度时会重复遍历
     * 时间复杂度：O(n^2)
     */
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        while (root!= null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            TreeNode inNode = stack.peek();
            // 右结点为null或已经遍历过
            if (inNode.right == null || inNode.right == pre) {
                // 比较左右子树的高度差，输出
                if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
                    return false;
                }
                stack.pop();
                pre = inNode;
                root = null;// 当前结点下，没有要遍历的结点了
            } else {
                root = inNode.right;// 右结点还没遍历，遍历右结点
            }
        }
        return true;
    }

    /**
     * 层序遍历，求结点的高度
     */
    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode poll = deque.poll();
                if (poll.left != null) {
                    deque.offer(poll.left);
                }
                if (poll.right != null) {
                    deque.offer(poll.right);
                }
            }
        }
        return depth;
    }
}

解法三：迭代优化

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
   /**
     * 优化迭代法，针对暴力迭代法的getHeight方法做优化，利用TreeNode.val来保存当前结点的高度，这样就不会有重复遍历
     * 获取高度算法时间复杂度可以降到O(1)，总的时间复杂度降为O(n)。
     * 时间复杂度：O(n)
     */
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            TreeNode inNode = stack.peek();
            // 右结点为null或已经遍历过
            if (inNode.right == null || inNode.right == pre) {
                // 输出
                if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
                    return false;
                }
                stack.pop();
                pre = inNode;
                root = null;// 当前结点下，没有要遍历的结点了
            } else {
                root = inNode.right;// 右结点还没遍历，遍历右结点
            }
        }
        return true;
    }

    /**
     * 求结点的高度
     */
    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = root.left != null ? root.left.val : 0;
        int rightHeight = root.right != null ? root.right.val : 0;
        int height = Math.max(leftHeight, rightHeight) + 1;
        root.val = height;// 用TreeNode.val来保存当前结点的高度
        return height;
    }
}

257.二叉树的所有路径

题目链接：https://leetcode.cn/problems/binary-tree-paths/description/

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

解题思路

思路一：（DFS）递归

• 沿着一条子树一路遍历，用 StringBuilder 存储每个子树的节点值

• 当 当前节点 没有子节点时，说明到达了叶子节点，用 list 存储整条 StringBuilder

• 返回 当前节点的父节点 继续遍历（回溯）

• 最后返回 list 即可

思路二：迭代

• 通过栈获取 一个 二叉树的 节点以及节点值

• 依次弹出节点和节点值，用path 存储值，用node存储节点，开始判断

  • 如果二叉树当前节点是 叶子节点，用 result 数组存储 path
  • 如果没达到叶子节点，则压入栈的 值 为 path + "->" + node.left.val 或者 path + "->" + node.right.val

• 遍历结束，返回 result

详细代码

解法一：递归（回溯）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<String> list = new ArrayList<>();
    List<Integer> paths = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        DFSTraversal(root);
        return list;
    }
    public void DFSTraversal(TreeNode node){
        if(node == null){
            return;
        }
        paths.add(node.val);

        //输出条件
        if(node.left == null && node.right == null){
            StringBuilder sb = new StringBuilder();
            for(int i = 0; i < paths.size() - 1; i++){
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));
            list.add(sb.toString());
        }

        if(node.left != null){
            DFSTraversal(node.left);
            paths.remove(paths.size() - 1);//回溯
        }
        if(node.right != null){
            DFSTraversal(node.right);
            paths.remove(paths.size() - 1);
        }
    }
}

解法二：迭代

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Stack<Object> stack = new Stack<>();
    List<String> res = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        if(root == null){
            return res;
        }

        stack.push(root);
        stack.push(root.val + "");

        while(!stack.isEmpty()){
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();

            if(node.left == null && node.right == null){
                res.add(path);
            }

            if(node.left != null){
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
            if(node.right != null){
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
            
        }
        return res;
    }
}

404. 左叶子之和

题目链接：https://leetcode.cn/problems/sum-of-left-leaves/description/

给定二叉树的根节点 root ，返回所有左叶子之和。

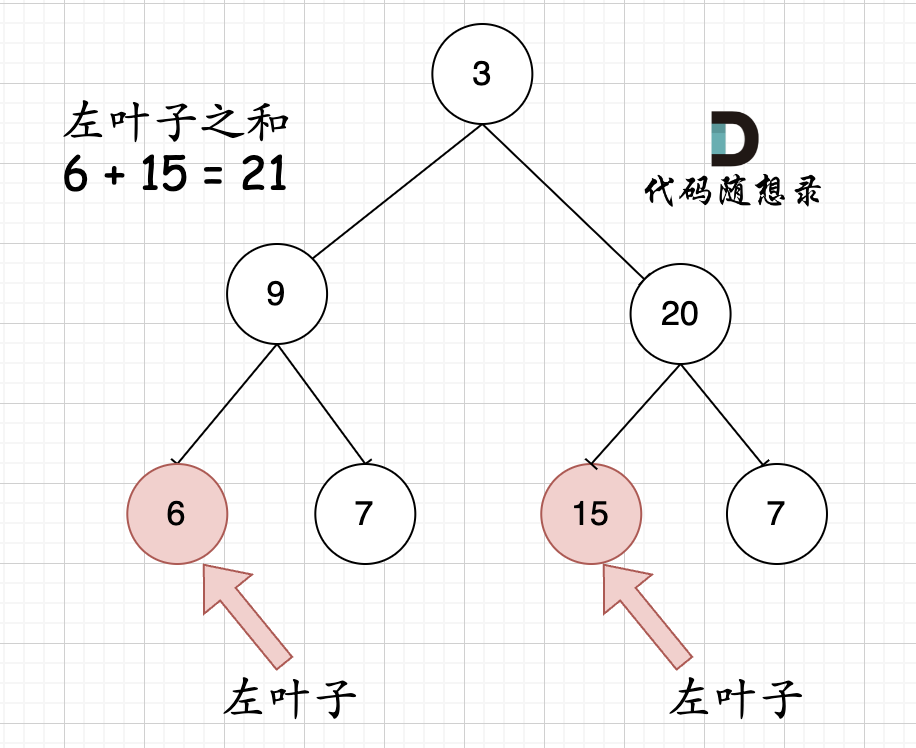
左叶子定义

节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

解题思路

思路一：递归

• 分别对 left 和 right 节点进行递归遍历

• 定义 左叶子节点 mid

  • 要满足 root.left != null && root.left.left == null && root.left.right == null

• 返回 sum = mid + left + right

思路二：迭代

• 用 栈 遍历每个节点元素

• 找到满足 root.left != null && root.left.left == null && root.left.right == null的节点 root

  • 如果找到了这个节点 root，说明它的左节点root.left 必为 左叶子节点

• 累加 root.left.val 后返回

思路三：层序遍历迭代

• 具体解法和 思路二 一致
• 只是使用了 队列 进行遍历

详细代码

解法一：递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = sumOfLeftLeaves(root.left);
        int right = sumOfLeftLeaves(root.right);

        int mid = 0;
        if(root.left != null && root.left.left == null && root.left.right == null){
            mid = root.left.val;//左叶子节点
        }
        int sum = mid + left + right;
        return sum;
    }
}

解法二：栈迭代

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Stack<TreeNode> stack = new Stack<>();

    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null){
            return 0;
        }
        stack.push(root);
        int sum = 0;
        while(!stack.isEmpty()){
            TreeNode tmpNode = stack.pop();
            if(tmpNode.left != null && tmpNode.left.left == null && tmpNode.left.right == null){
                sum += tmpNode.left.val;
            }
            if(tmpNode.left != null){
                stack.push(tmpNode.left);
            }
            if(tmpNode.right != null){
                stack.push(tmpNode.right);
            }
        }
        return sum;
    }
}

解法三：层序遍历迭代（队列）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Queue<TreeNode> queue = new LinkedList<>();
    int sum = 0;

    public int sumOfLeftLeaves(TreeNode root) {
        BFS(root);
        return sum;
    }

    public void BFS(TreeNode node){
        if(node == null){
            return;
        }
        queue.offer(node);

        while(!queue.isEmpty()){
            int size = queue.size();
            while(size-- > 0){
                TreeNode tmpNode = queue.poll();
                if(tmpNode.left != null){
                    queue.offer(tmpNode.left);
                    if(tmpNode.left.left == null && tmpNode.left.right == null){
                    sum += tmpNode.left.val;
                    }
                }
                if(tmpNode.right != null){
                    queue.offer(tmpNode.right);
                }
            }
        }
    }
}