算法训练营(day14)
二叉树理论基础
二叉树的种类
满二叉树
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
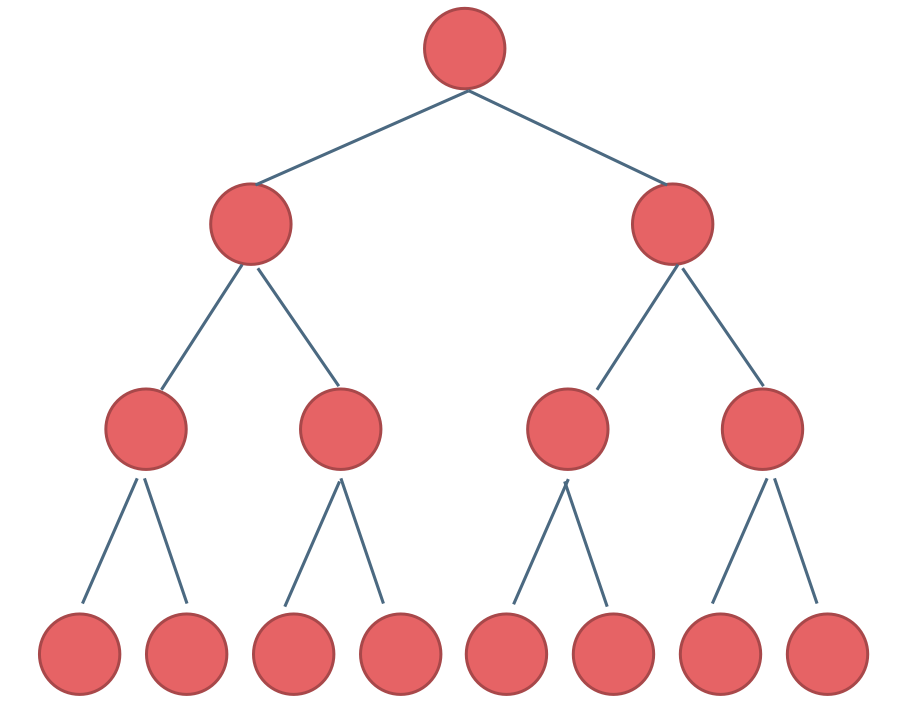
完全二叉树
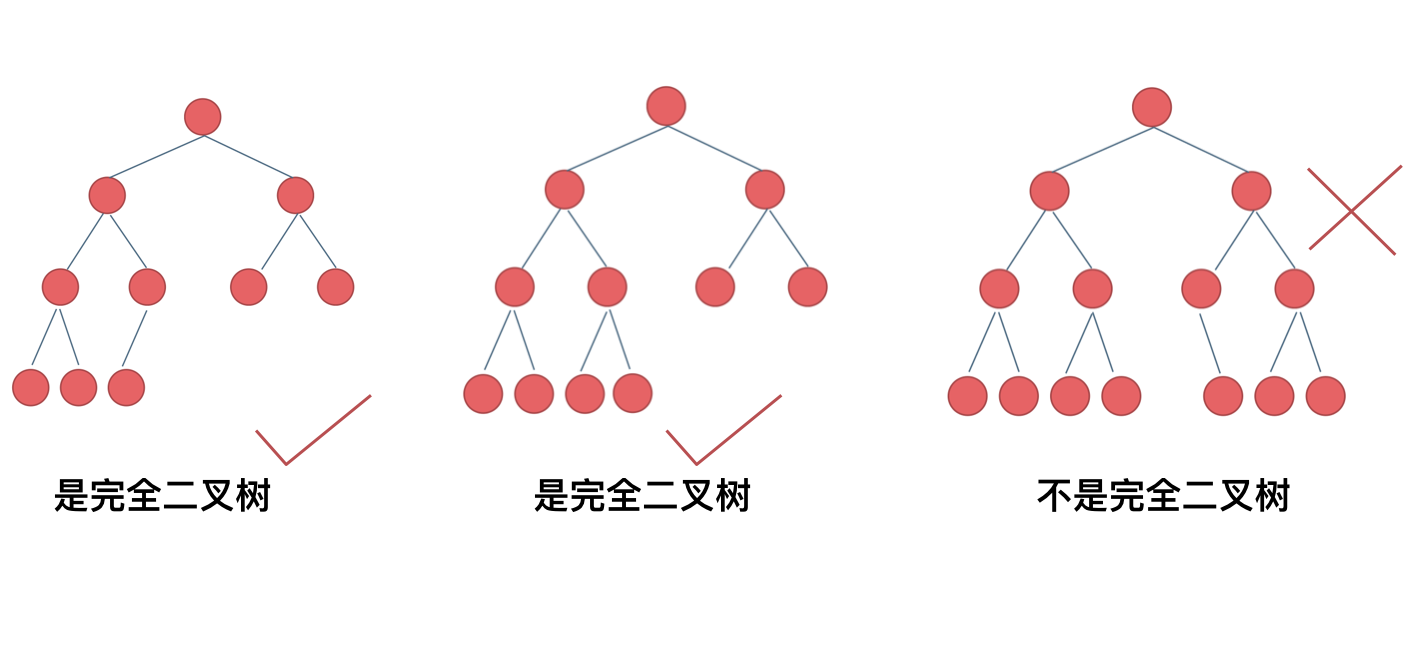
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
二叉搜索树
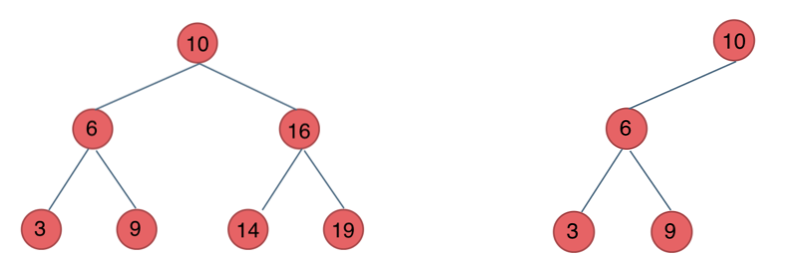
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
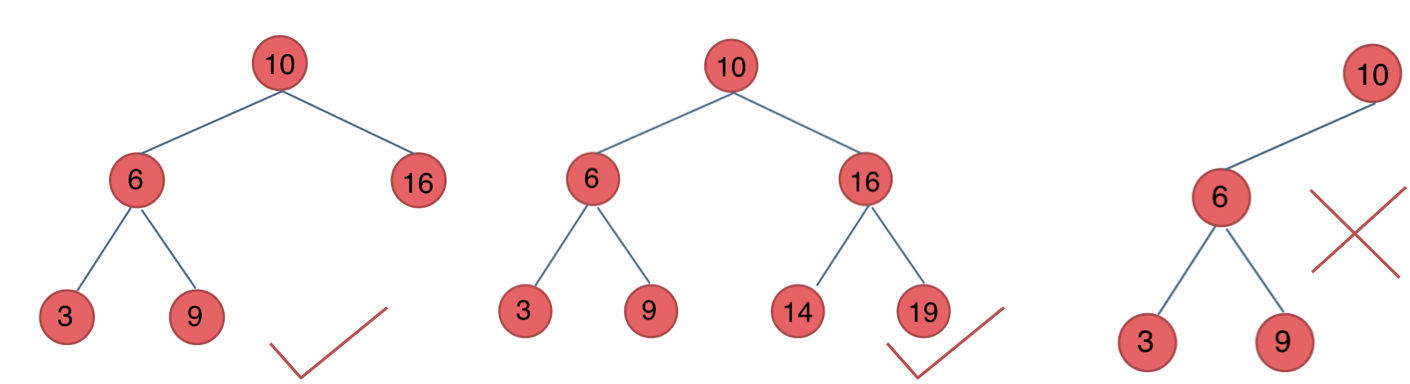
平衡二叉搜索树
空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。链式存储方式就用指针, 顺序存储的方式就是用数组。
如果使用数组存储二叉树,有 如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历方式
二叉树主要有两种遍历方式:
- 深度优先遍历(dfs):先往深走,遇到叶子节点再往回走
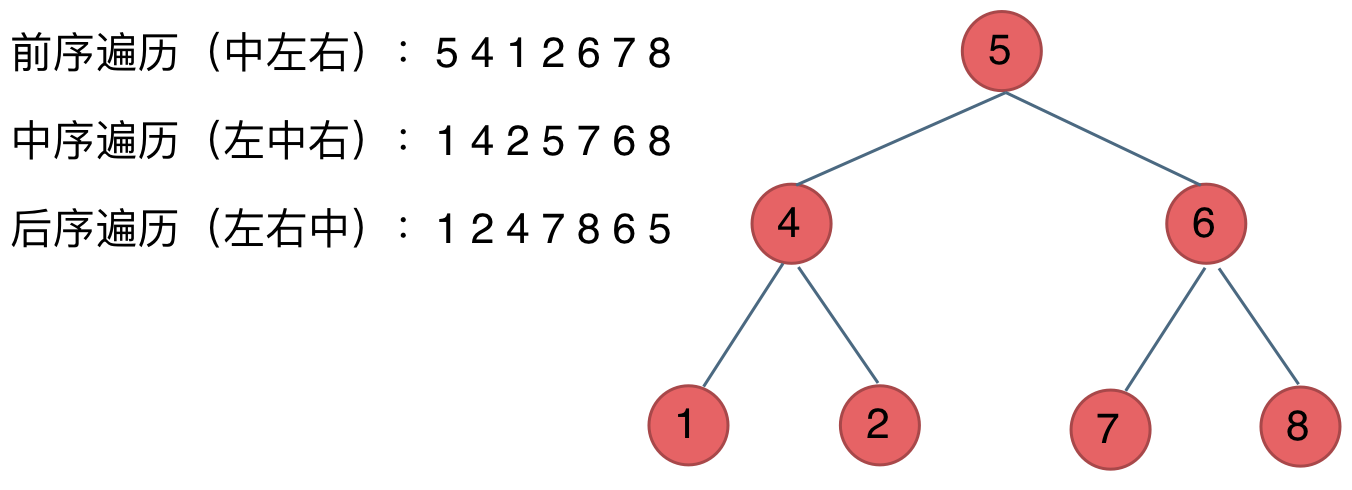
- 前序遍历(递归,迭代)–> 中左右
- 中序遍历(递归,迭代)–> 左中右
- 后序遍历(递归,迭代)–> 左右中
- 广度优先遍历(bfs):一层一层的遍历
二叉树的代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
|
144. 二叉树的前序遍历
题目链接:https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
解题思路
解题过程:
- 前序遍历:中左右
详细代码
解法一:递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
preorder(root, res);
return res;
}
public void preorder(TreeNode root, List<Integer> res){
if(root == null){
return;
}
res.add(root.val);
preorder(root.left, res);
preorder(root.right, res);
}
}
|
解法二:迭代遍历(注意 栈 先进后出)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
List<Integer> res = new LinkedList<>();
if(root != null){
stack.push(root);
}
while(!stack.isEmpty()){
TreeNode node = stack.peek();
if(node != null){
stack.pop();
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}
stack.push(node);
stack.push(null);
}else{
stack.pop();
node = stack.peek();
stack.pop();
res.add(node.val);
}
}
return res;
}
}
|
94. 二叉树的中序遍历
题目链接:https://leetcode.cn/problems/binary-tree-inorder-traversal/description/
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
解题思路
解题过程:
- 中序遍历:左中右
详细代码
解法一:递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
public void inorder(TreeNode root, List<Integer> res){
if(root == null){
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
|
解法二:迭代遍历(注意 栈 先进后出)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
List<Integer> res = new LinkedList<>();
if(root != null){
stack.push(root);
}
while(!stack.isEmpty()){
TreeNode node = stack.peek();
if(node != null){
stack.pop();
if(node.right != null){
stack.push(node.right);
}
stack.push(node);
stack.push(null);
if(node.left != null){
stack.push(node.left);
}
}else{
stack.pop();
node = stack.peek();
stack.pop();
res.add(node.val);
}
}
return res;
}
}
|
145. 二叉树的后序遍历
题目链接:https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
解题思路
解题过程:
- 后序遍历:左右中
详细代码
解法一:递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
public void postorder(TreeNode root, List<Integer> res){
if(root == null){
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
}
|
解法二:迭代遍历(注意 栈 先进后出)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
List<Integer> res = new LinkedList<>();
if(root != null){
stack.push(root);
}
while(!stack.isEmpty()){
TreeNode node = stack.peek();
if(node != null){
stack.pop();
stack.push(node);
stack.push(null);
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}
}else{
stack.pop();
node = stack.peek();
stack.pop();
res.add(node.val);
}
}
return res;
}
}
|






